선형 대수 : 연립 방정식

* 선형대수학의 기본 요소 : 각 구성요소의 포함된 구성 요소의 개수에 따라 관점이 달라짐.

- Scala : 하나의 숫자

- Vector : 숫자의 정렬된 목록

- Matrix : 2차원의 숫자 배열

​

​

* 표기법과 핵심 작업

- 스칼라는 소문자로, 벡터는 굵은 소문자로, 행렬은 대문자로 표시

- 행렬의 열과 행의 크기가 같은 경우 정사각 행렬이라고 한다. Square Matrix. 그 외의 경우는 직사각 행렬이라고 하며, Rectangular Matrix라고 합니다.

- 전치(Transpose) : 원래의 행렬을 왼쪽 위에서 오른쪽 아래로 시작하여 대각선을 따라 반전시키거나 시킨 것

- 벡터와 행렬간의 곱셉과 덧셈

· 2개의 주어진 행렬의 가산은 2개의 행렬 요소 -별 가산으로 계산

· 따라서 같은 크기의 행렬이 덧셈이 가능하며 결과도 같은 크기이다.

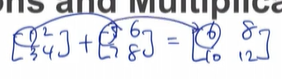
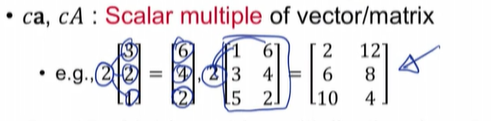
· 벡터와 행렬의 스칼라 곱셈은 벡터의 각 요소 값에 공통 스칼라 값을 곱해서 구한다.

· 왼쪽에서 행 벡터, 오른쪽에서 열 벡터를 선택

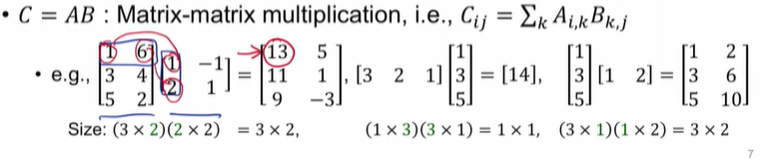
· 따라서 곱셉을 하려면 왼쪽 행렬의 열 크기와 오른쪽 행렬의 행 크기가 같아야함.

· 2번째 케이스처럼 값이 스칼라값이 되거나 값이 더 작아지는 경우 내적이라고 함.

· 3번쨰 케이스처럼 핀 벡터로부터 확장된 행렬을 외적이라고 함.

· 행렬 곱셈은 교환가능하지 않다. A X B는 B X A와 같지않다.

​

​

* 선형 방정식

- 모든 계수 값가 변수, 변수를 단일 벡터로 수집하여 위의 보기처럼 간략화할 수 있다.

​

​

* 선형 시스템과 선형 시스템을 해결하는 방법

- 선형 시스템은 X1에서 xn까지의 동일한 변수를 포함하는 하나 이상의 선형 방정식의 모음

Ex)

 

· X를 푸는 방법을 위해

항등 행렬이라고 하는 특수 행렬을 먼저 논의// 항등 행렬은 대각선 행이 모두 1이고 다른 항이 0인 정사각 행렬

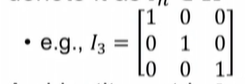
· 종종 I_n으로 표시. 이는 n x n 항등 행렬이라는 뜻

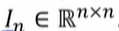
· 이 항등 행렬을 곱한 후에도 벡터 x를 보존한다는 중요한 특성이 있다. 따라서 이것이 3차원 입체의 경우에 해당하는지 확인해볼 수 있다.

​

​

- 역행렬

 

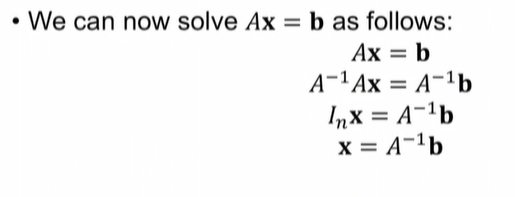
* 주어진 선형 시스템에 대한 솔루션이 전혀 없거나 여러 개인 경우

- 집합이 역집합이 없다면? 큰 문제 야기. 유니크한 솔루션이나 모델을 제기할 수 없음을 의미.

 

 

 

- 방정식보다 변수가 많을 경우 불확실한 시스템이라고 한다.

- 방정식이 변수보다 많을 경우 : 지나치게 결정된 시스템